René Descartes encontró un método para indicar el número de raíces positivas en un polinomio. Esta regla dice lo siguiente:
"El número de raíces reales positivas de un polinomio f(x)=0 es igual al número de cambios de signo de término a término (variaciones) de f(x) o es menor que este en un numero par. El numero de raíces negativas es igual al número de variaciones de f(-x) o es menor que este en un numero par"
La regla de los signos de Descartes nos ayuda a identificar el número posible de raices reales de un polinomio p(x) sin gráfica o resolverlas realmente.La
regla establece que el número posible de las raíces positivas de un
polinomio es igual al número de cambios de signo en los coeficientes de
los términos o menor que los cambios de signo por un múltiplo de 2.Por
ejemplo, si hay 3 cambios de signo en los coeficientes de los términos
del polinomio, entonces el número posible de raíces positivas del
polinomiao es 3 o 1.[Antes
de aplicar la regla de los signos de Descartes, asegúrese de arreglar
los términos del polinomio en orden descendente de exponente]
Ejemplo:
Encuentre el número de las raíces positivas del polinomio. x3 + 3 x2 – x – x4– 2
Arregle los términos del polinomio en orden descendente de los exponentes: – x4 + x3 + 3 x2– x – 2
Cuente el número de cambios de signo:
Hay 2 cambios de signo en el polinomio, así que el número posible de raíces positivas del polinomio es 2 o 0.
División Sintética.
La división sintética es un algoritmo
para rápidamente dividir polinomios cuando el divisor está en el x-r de la forma. La división sintética formalmente
se llama la regla de Ruffini. La división sintética es de uso
general verificar raíces de un polinomio.
Ejemplo 1
| Paso | Ecuaciones | Descripción |
|---|---|---|
| 1 | 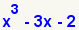 | Éste es el dividendo. |
| 2 |  | Éste es el divisor. |
| 3 | 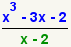 | Ésta es la operación que será realizada. |
| 4 | 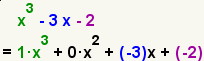 | Identifique los coeficientes implicados y complételos. La aplicación de la propiedad de multiplicarse por 1 al término x3 da un coeficiente implicado es 1. Note que no hay término x2. Aplicando la propiedad de multiplicarse por 0 entonces la propiedad de agregar 0 al término x2 da 0·x2. |
| 5 | 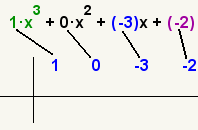 | Copie los coeficientes en la tapa de una rejilla. |
| 6 |  | Copie opuesto del término constante del divisor en la rejilla a la izquierda. |
| 7 |  | Copie abajo del coeficiente del término con el grado más grande. En este caso, el coeficiente es 1. |
| 8 | 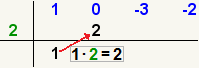 | Multiplique el primer número en la parte inferior por el número a la izquierda. Ponga el resultado en la 2da fila, la columna siguiente a la derecha. |
| 9 | 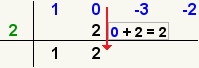 | Agregue los números en las primeras dos filas de la columna siguiente. Ponga el resultado en la 3ro fila. |
| 10 | 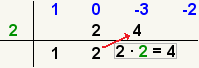 | Multiplique el número en la 3ro fila de la columna actual por el número a la izquierda. Ponga el resultado en la 2da fila, la columna siguiente a la derecha. |
| 11 | 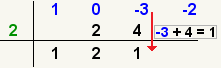 | Agregue los números en las primeras dos filas de la columna siguiente. Ponga el resultado en la 3ro fila. |
| 12 |  | Multiplique el número en la 3ro fila de la columna actual por el número a la izquierda. Ponga el resultado en la 2da fila, la columna siguiente a la derecha. |
| 13 |  | Agregue los números en las primeras dos filas de la columna siguiente. Ponga el resultado en la 3ro fila. |
| 14 | 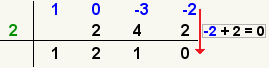 | Multiplique el número en la 3ro fila de la columna actual por el número a la izquierda. Ponga el resultado en la 2da fila, la columna siguiente a la derecha. |
| 15 | 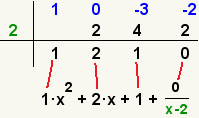 | Copie los coeficientes del resultado en un polinomio. |
| 16 | 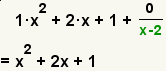 | Simplifique el polinomio. |
| 17 | 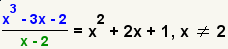 | Aquí está el problema con el resultado. |
| 18 | 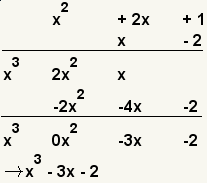 | Compruebe el trabajo multiplicando el resultado por el divisor. |
Teorema del Factor.
En álgebra, el teorema del factor sirve para encontrar los factores de un polinomio (una expresión en la cual los términos sólo son sumados, sustraídos o multiplicados, e.g. x2 + 6x + 6). Es un caso especial del teorema del resto.
El teorema del factor establece que un polinomio f(x) tiene un factor (x − k) si y sólo si k es una raíz de f(x), es decir que f(k) = 0.
Ejemplo:
Si se desea encontrar los factores de x3 + 7x2 + 8x + 2, para ello se podría tantear un primer factor, (x − a). Si el resultado de sustituir a en el polinomio es igual a 0, se sabe que hay un factor. ¿Es (x − 1) un factor? Para saberlo, se sustituye x = 1 en el polinomio:
Cómo esta operación da 18 (y no 0), (x − 1) no es un factor de x3 + 7x2 + 8x + 2. Así que ahora se prueba con (x + 1) (sustituyendo x = − 1 en el polinomio):
.
Que da como resultado 0. Por tanto, x − ( − 1), que es equivalente a x + 1, es un factor, y -1 es una raíz de x3 + 7x2 + 8x + 2.
En álgebra, el teorema del factor sirve para encontrar los factores de un polinomio (una expresión en la cual los términos sólo son sumados, sustraídos o multiplicados, e.g. x2 + 6x + 6). Es un caso especial del teorema del resto.
El teorema del factor establece que un polinomio f(x) tiene un factor (x − k) si y sólo si k es una raíz de f(x), es decir que f(k) = 0.
Ejemplo:
Si se desea encontrar los factores de x3 + 7x2 + 8x + 2, para ello se podría tantear un primer factor, (x − a). Si el resultado de sustituir a en el polinomio es igual a 0, se sabe que hay un factor. ¿Es (x − 1) un factor? Para saberlo, se sustituye x = 1 en el polinomio:
Cómo esta operación da 18 (y no 0), (x − 1) no es un factor de x3 + 7x2 + 8x + 2. Así que ahora se prueba con (x + 1) (sustituyendo x = − 1 en el polinomio):
.
Que da como resultado 0. Por tanto, x − ( − 1), que es equivalente a x + 1, es un factor, y -1 es una raíz de x3 + 7x2 + 8x + 2.
Fuentes de información:
http://analisis-numerico-horacio.blogspot.mx/2012/03/ley-de-los-signos-de-descartes.html
http://www.allmathwords.org/es/s/syntheticdivision.html
http://www.allmathwords.org/es/s/syntheticdivision.html
No comments:
Post a Comment