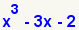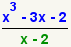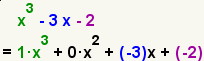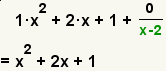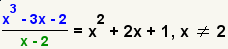En
algunos casos es conveniente factorizar los polinomios mediante divisiones
sintéticas (regla de Ruffini). Esta regla se aplica en polinomios cuyos
factores son de la forma (x ± a)
Esta
regla nos dice que “un polinomio tiene por factor (x ± a) si al reemplazar el
valor x por “a” en el polinomio, el resultado es cero. El valor de “a” de los
posibles factores de la expresión, es un divisor del término independiente del
polinomio”.
Ejemplo: x4+6x3+x2-24x+16
El posible valor de
“a” deber ser divisor del término
independiente es este caso 16
16 tiene por
divisor 1,2,3,4,8,16. cualquiera de ellos puede ser el que haga cero la
expresión
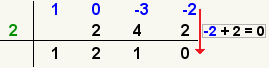
Para
dividir en forma sintética, tomamos los coeficientes del polinomio y dividimos
para los divisores de 16.
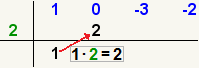
Probamos con 2: Si x4+6x3+x2-24x+16, Sus coeficientes en
orden son:
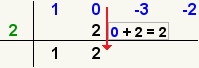
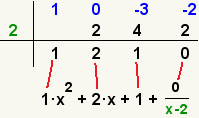
1. Bajas el primer cociente y multiplicas por el divisor. Ubicas
bajo el 2do.cociente para sumar o restar según sea el caso
1 6 1 -24 16 2
2 16 34 20
1 8 17 10 36 NO
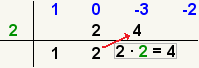
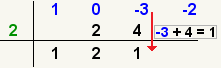
2. Multiplicas por el divisor y ubicas bajo el
3er.coeficiente y asi sucesivamente hasta terminar todos los coeficientes
1 6 1 -24 16 -4
-4 -8 28 -16
|
|
1 2 -7 4 0 SI
Coeficientes resultantes
(x3+2x2-7x+4)
(x+4)
4. Si obtienes cero entonces ese divisor es el
valor de la variable y para que sea cero el factor será con el signo contrario
En nuestro caso nos salió para -4 entonces el factor es (x+4)
1 2 -7 4 1
1 3 -4
1 3 -4 0 SI
|
(x+4) (x-1) (x-1) (x+4)
= (x+4)2 (x-1)2
Comprobación como nos dio
cero cuando a=-4 reemplazamos en el polinomio original.
= x4 + 6x3 + x2
- 24x + 16
= (-4)4 + 6(-4) + (-4)2
- 24(-4) + 16
= 256-384+16+96+16
= 0 es
lo que debe suceder
Teorema del Resto.
Si C(x) es el cociente y R(x)
el resto de la división de un polinomio cualquiera
P(x) entre el binomio (x
– a), aplicando el algoritmo de la división:
P(x) = C(x) ·
(x – a) + R(x)
Luego, el valor numérico de P(x), para
x = a, es igual al resto de su división
entre x – a, es decir:
P(a) = C(a) · (a – a) + R(a)
= R(a)
Y este resultado se conoce como teorema del
resto.
Este teorema nos permite averiguar el resto de la
división de un polinomio P(x)
entre otro de la forma x – a, sin necesidad
de efectuar esta división.
De este teorema se deduce que un polinomio P(x)
es divisible por x – a si y
solo a es una raíz del polinomio, es decir, si y
solo si P(a) = 0.
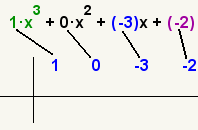
Así, por ejemplo, el resto de la división de P(x)
= x3
+ 3x2 – 7x – 3 entre x –
2
es:
P(2) = (2)3 + 3 · (2)2 – 7 · (2) – 3 = 3
De donde se deduce que esa división no es exacta
y, por tanto, x – 2 no es un
divisor
de P(x).
Teorema Fundamental del álgebra
El teorema fundamental del
álgebra (TFA) dice que "toda ecuación polinómica
de grado n con coe.cientes
complejos tiene n raíces complejas".
De hecho existen múltiples
formulaciones equivalentes; por ejemplo que todo
polinomio real puede expresarse
como producto de factores reales lineales y
cuadráticos.
Fuentes de información: